A weighted average is the average of values which are scaled by importance. In other words, it's a way to calculate an average where some points contribute more than others.
The formula for computing a weighted average is:
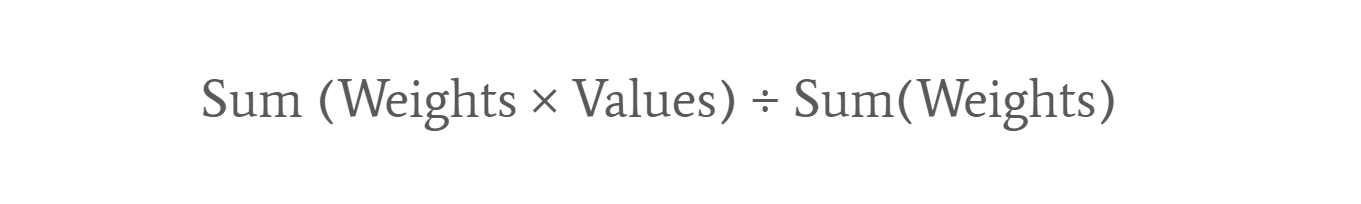
For example, say we have data from a grocery store which sells 3 items (apples, pears and oranges), and the items are ordered from 2 suppliers (A & B):
Supplier | Item | Cost per item | Quantity |
A | Apples | £0.50 | 10 |
A | Pears | £0.30 | 12 |
A | Oranges | £0.40 | 15 |
B | Apples | £0.70 | 6 |
B | Pears | £0.50 | 4 |
B | Oranges | £0.60 | 3 |
The average cost per item is:
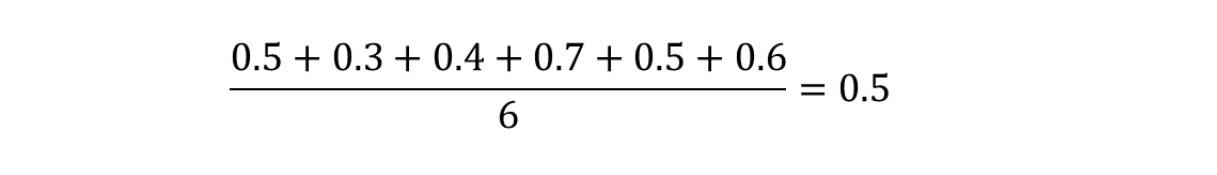
The weighted average cost per item would take into account how many items has been ordered from each supplier. This means we'll be using the Quantity as our weight. So, the weighted average cost per items would be:
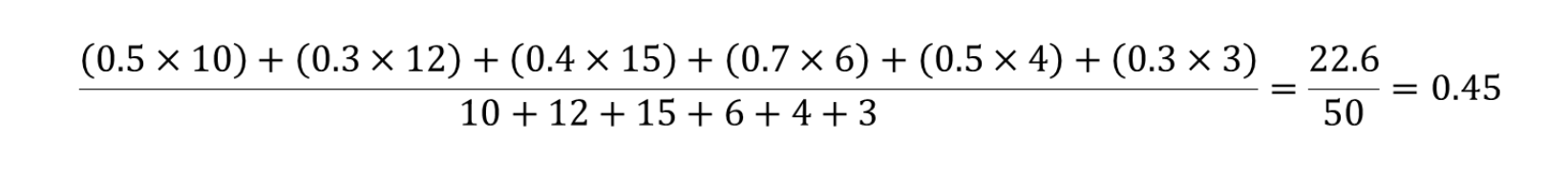
Now, let's look at other examples and how we would compute weighted averages in Tableau.
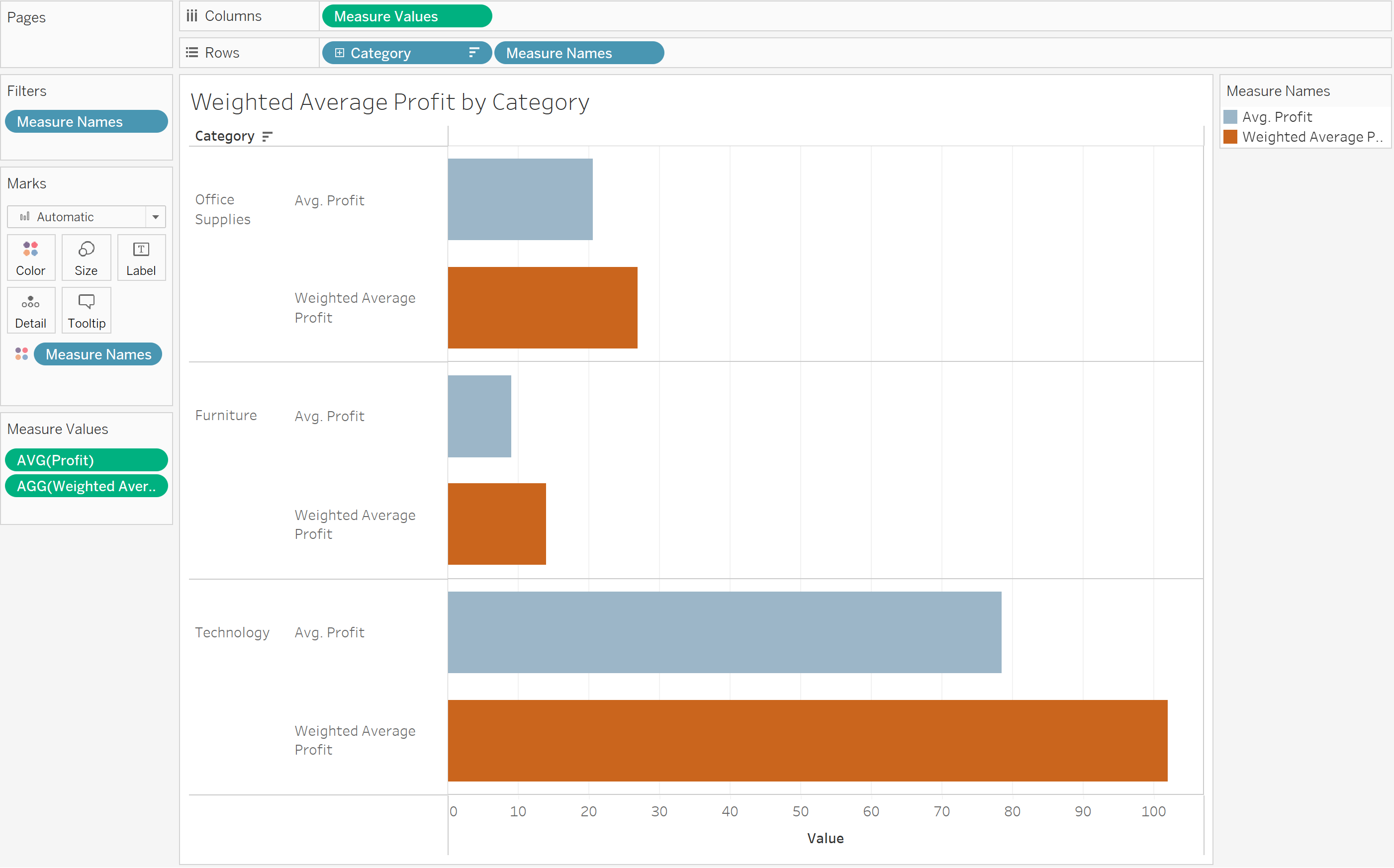
Example 1: Using Sample Superstore data, find the weighted average profit per product and order by region
Here, we compute the weighted average profit using a calculated field (where the weight is quantity) with the following syntax:
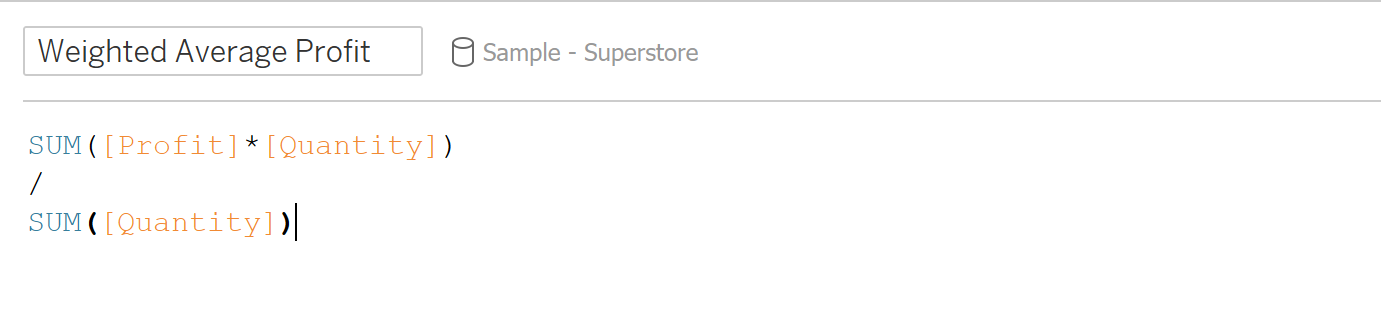
When we visualize both the weighted average profit and the average profit, we can see where they differ:
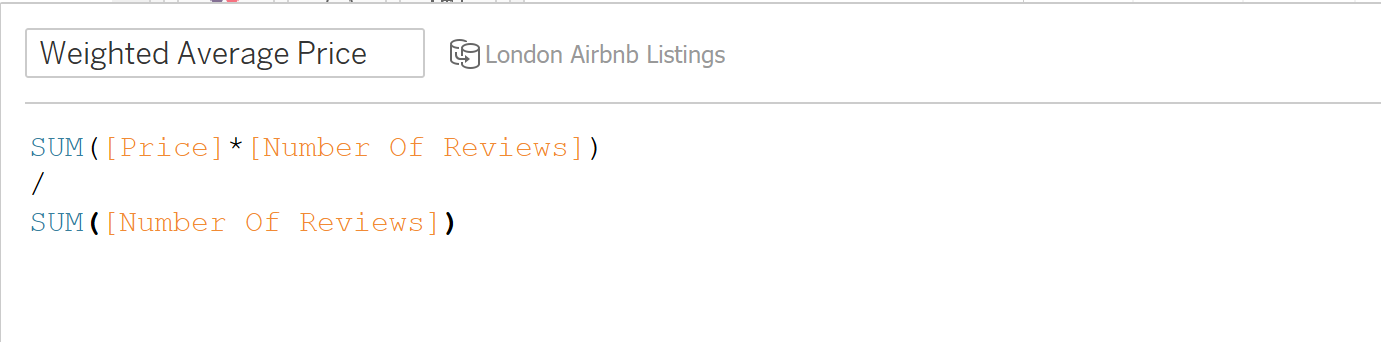
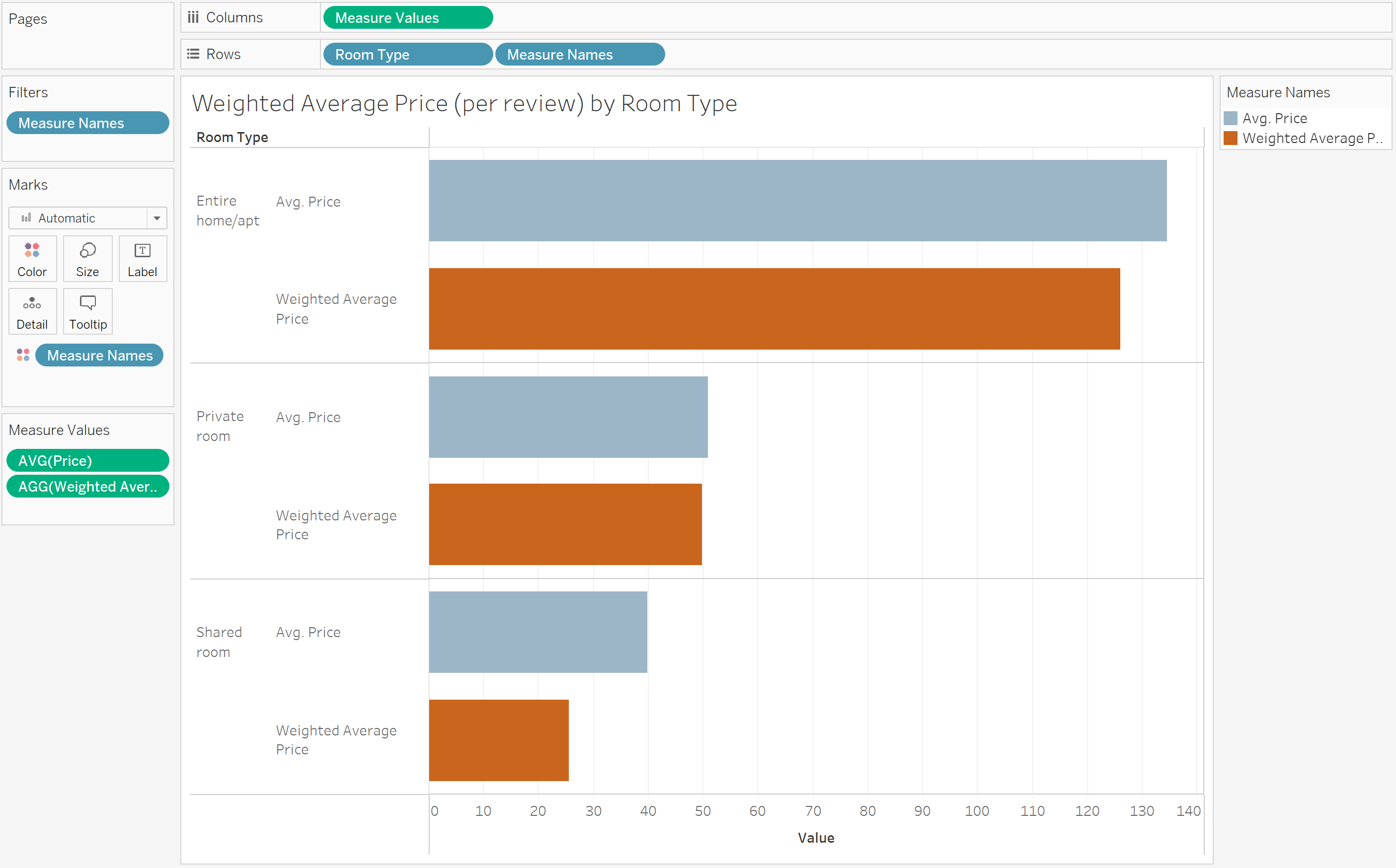
Example 2: Using London AirBnB Listings data, find the weighted average price per review and order by room type
In this example, the syntax for our calculated field (where the weight is the number of reviews) would be:
Again, let's visualize to see how the average price compares to the weighted average price:
Why are weighted averages important?
Overall, they offer a more nuanced and accurate representation of data compared to simple averages. Here are some key reasons why weighted averages are valuable:
- Accounting for Variability in Data:
Weighted averages are particularly beneficial when dealing with datasets where different values have varying degrees of importance or significance. Assigning weights allows you to account for this variability and ensures that the resulting average reflects the true impact of each value on the overall calculation. - Reflecting Real-world Scenarios:
In many real-world scenarios, not all data points contribute equally to an aggregate value. Weighted averages help capture the influence of certain elements more accurately, mirroring the actual impact of those elements in practical situations. For instance, in financial analysis, larger investments or transactions may have a more substantial effect on the overall performance. - Improving Accuracy in Aggregated Measures:
Weighted averages are crucial when dealing with measures that involve both quantity and quality. By assigning appropriate weights, you can improve the accuracy of aggregated measures, ensuring that the calculated average reflects the true average value considering the influence of different factors. - Dealing with Heterogeneous Data:
When working with heterogeneous datasets, where different subsets of data have distinct characteristics or magnitudes, weighted averages provide a more reliable measure of central tendency. This is especially important in fields such as economics, where diverse factors contribute to overall trends. - Enhancing Decision-making:
Weighted averages are essential in decision-making processes, as they offer a more informed perspective. Whether it's calculating grades in education, determining portfolio returns in finance, or evaluating product performance in sales, weighted averages enable decision-makers to consider the relative importance of different components. - Accurate Performance Assessment:
In business and finance, weighted averages are frequently used to assess performance metrics. For example, calculating the weighted average return on investment (ROI) helps investors evaluate the overall performance of a portfolio by considering the proportion of investment in each asset.
In summary, weighted averages provide a robust method for aggregating data, especially in situations where not all values contribute equally to the final result. Their ability to account for variations in importance makes them a valuable tool in statistical analysis, decision-making, and understanding the true impact of different factors in diverse datasets.
